temperature和top-p采样

在生成文本时，调整采样策略可以显著影响输出的多样性。两种常用的方法是temperature采样和top-p采样。 temperature和Top-p都是

高->随机，有创造力。

低->确定，偏向保守。

原理

大模型核心任务是预测下一个最可能出现的词，该过程分为生成分数、转换概率、加权采样三个关键步骤。

生成分数

大模型会为其词汇表中所有词（数量通常为几万到几十万）打分，该分数在 AI 领域称为 logit。以用户问题 “可以给我推荐一个讲 ai 的技术频道吗？” 为例，模型会对相关词进行打分，实际应用中通常展示分数最高的前几个词。

转换概率

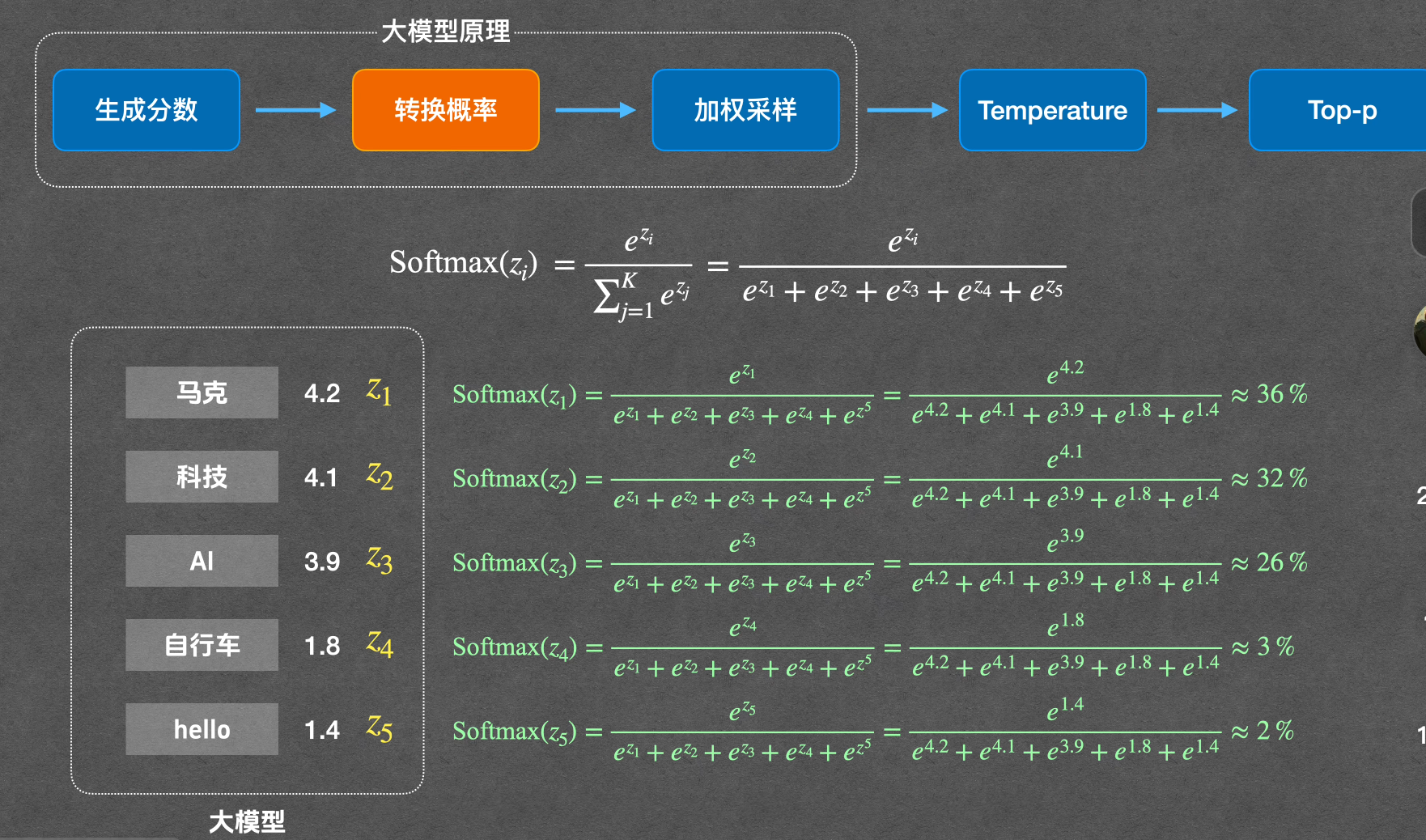
通过 softmax 函数将分数转换为概率，公式为

$$ \sigma(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{K} e^{z_j}} $$

其中zi为第 i 个词的分数，K 为词的总量。转换后得到每个词的输出概率，使模型能按概率预测下一个词。

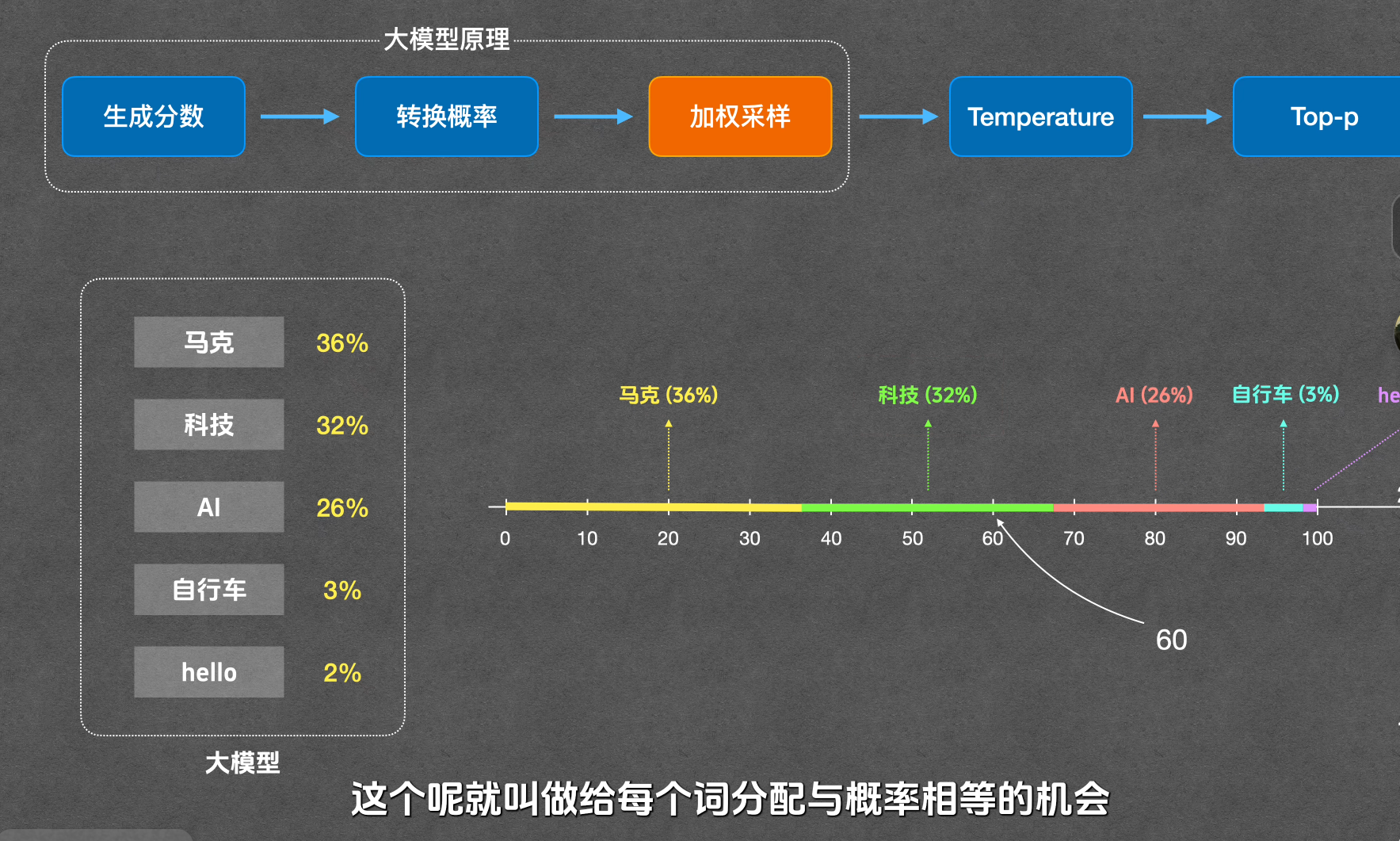
加权采样

根据概率生成预测值的过程称为加权采样。将每个词的概率对应分配到 0-100 的数轴区间，生成随机数，随机数落到哪个区间就选择对应词，以实现按概率输出。

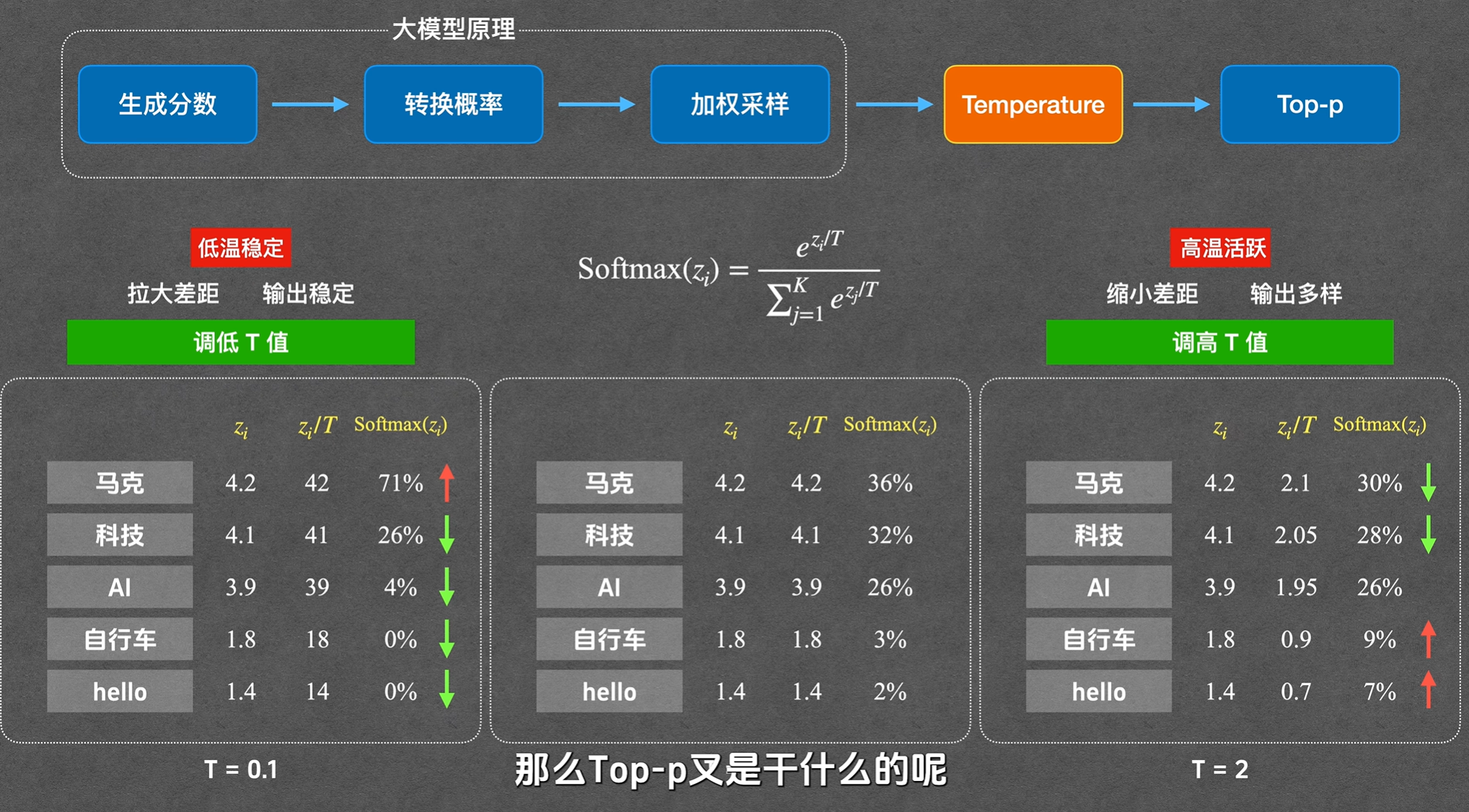
temperature 的作用

temperature（温度）与 softmax 函数相关，完整公式为

$$ \sigma(z_i) = \frac{e^{z_i / t}}{\sum_{j=1}^{K} e^{z_j / t}} $$

T为 temperature 值。T 值改变会影响不同词的概率差距，T越小，高分词与低分词概率差距越大，模型回答越保守稳定；T越大，概率差距越小，输出越随机多样。

如下图所示，T值越小，会将每个词之间概率差距拉大，更容易选到原先概率最高的那个词。所以低温稳定。

topp 的作用

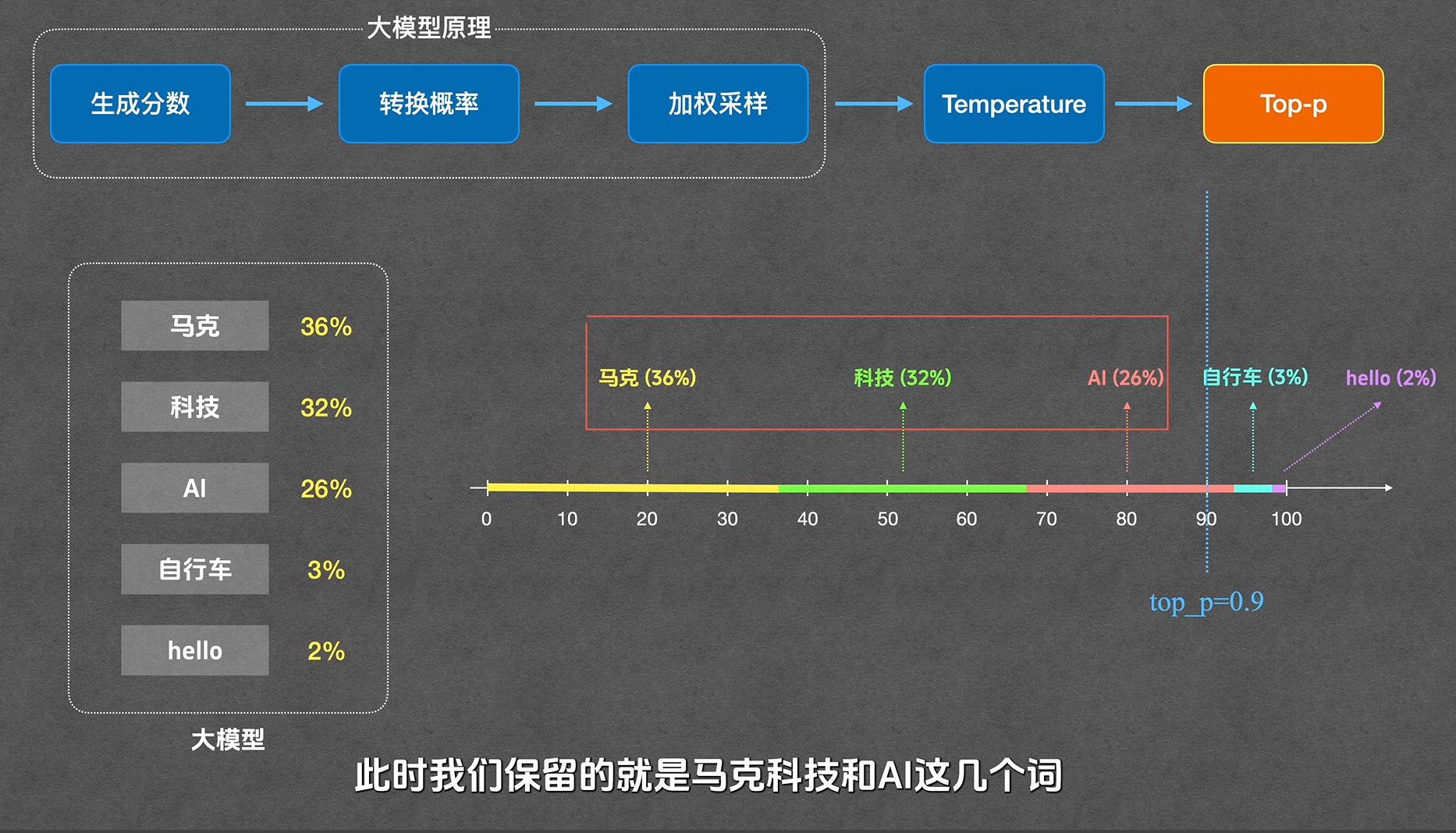
topp 全称 top cumulative probability（最高累加概率），是概率阈值。从概率最高的词开始累加，当累加概率达到设定阈值 p 时，保留这些词，丢弃剩余长尾词，再将保留词的概率按比例放大至总和为 1 后进行采样，用于切断低概率长尾词，保证回答不跑题。

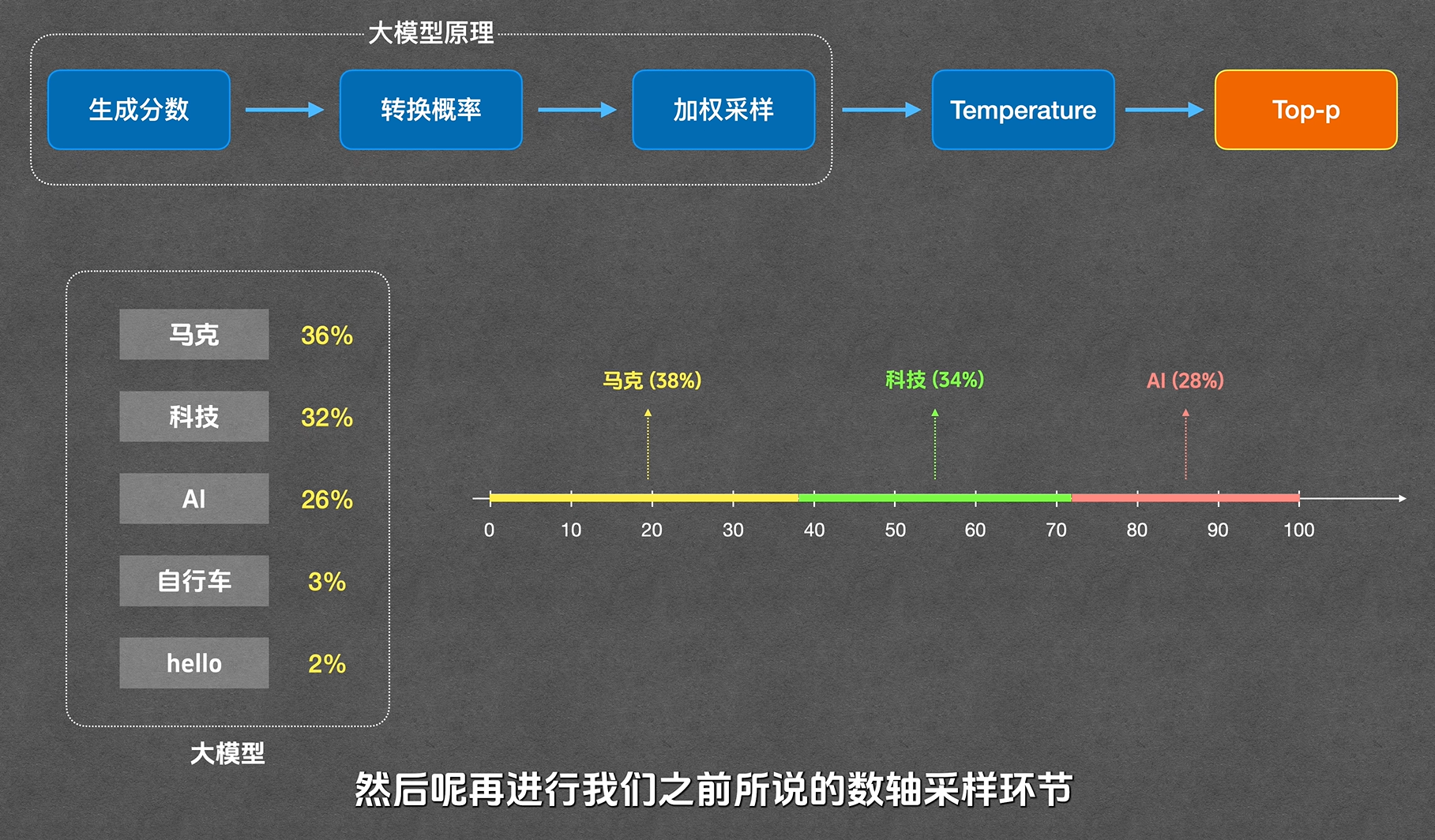
如图，当top_p=0.9时，“自行车”和“hello”这两个词就被丢弃掉了。接着需要将剩下的三个词按比例重新放大成100，再进行采样。如此一来，top_p越大，保留的词就越多，输出越多样。

通过自适应解码改进开放式文本生成

[2402.18223] 通过自适应解码改进开放式文本生成 — [2402.18223] Improving Open-Ended Text Generation via Adaptive Decoding

工作原理

H(X)：熵 (Entropy) —— 衡量“模型有多懵”

H(X) = −∑x ∈ Vp(x)log p(x)

  • 直观理解 ：熵是信息论中衡量“不确定性”的指标。p(x)是x归一化后的概率。
  • 在 LLM 中意味着什么 ：
    • 高熵（High Entropy） ：模型预测的概率分布很“平”，很多词的概率差不多（比如在写小说时，下一个词可能有几十种选法），模型处于“纠结”状态。
    • 低熵（Low Entropy） ：分布很“尖”，某个词的概率极大（比如填空“一加一等于_”），模型非常笃定。
  • 局限性 ：熵的绝对值受词表大小 |V| 的影响。一个拥有 10 万词表的模型和一个 3 万词表的模型，即便它们一样“懵”，算出来的 H(X) 也不一样，无法直接比较。

Conf(X)：置信度 —— 把“确定性”标准化

$$ Conf(X) = 1 + \frac{\sum p(x) \log p(x)}{\log|V|} = 1 - \frac{H(X)}{\log|V|} $$

  • 为什么这么改写 ：注意公式后半部分 $\frac{H(X)}{\log|V|}$。在词表为 |V| 的情况下，最大可能的熵是 log |V|（即所有词概率均等）。用当前的熵除以最大熵，得到的是一个 0 到 1 之间的比例 。
  • 物理意义 ：
  • Conf(X) ≈ 1 ：模型极其确定。
  • Conf(X) ≈ 0 ：模型完全在瞎猜（随机分布）。
  • 核心作用 ：它消除不同模型、不同词表大小之间的差异。无论你用 Llama-3 还是 Qwen，置信度 0.9 的含义是统一的，这为设置统一的阈值打下了基础。

ΔConf：增量置信度 —— 寻找“性价比”的拐点

这是这篇论文最精妙的地方。在解码的每一步，我们按概率从大到小逐个把 token 加入候选集 S。

$$ \Delta Conf = \frac{Conf_k(X) - Conf_{k-1}(X)}{\log|V|} $$

注意这里的隐含操作 ：当候选集里有 k 个词时，我们需要对这 k 个词的概率进行 重新归一化 （让它们的和等于 1），然后再计算这个局部集合的 Confk。

  • 它在衡量什么？
    • 它是“边际收益”。当我们把第 k 个词放入候选筐里时，这个动作是让整体意图更清晰了，还是让分布变得更混乱（注水）了？
  • 决策逻辑 ：
  1. 初始状态 ：候选集只有概率最高的词 x1，此时置信度很高。
  2. 添加词语 ：如果我们继续添加 x2, x3，如果这些词的概率也比较可观，它们和 x1 共同构成了一个有意义的“候选区间”，此时置信度可能还会上升或保持高位。
  3. 停止信号 ：当我们遇到一个概率很低的词（长尾词）时，把它强行塞进候选集会导致重新归一化后的分布迅速变“平”，此时 Confk 会显著下降，导致 ΔConf 变成负值或极小值。

举例说明

我们假设词表大小 |V| = 4（为了计算方便），因此 ln |V| = ln (4) ≈ 1.386。

模型预测的原始概率分布为：

  • w1: 0.80 (最想说的词)
  • w2: 0.15 (备选词)
  • w3: 0.04 (噪声)
  • w4: 0.01 (无意义)

第一步：计算 k = 1 时的状态

此时候选集 S1 = {w1}。

  1. 局部归一化： 由于只有一个词，它的概率变成 P′(w1) = 0.80/0.80 = 1.0。
  2. 计算熵 H1： H1 = −(1.0 × ln 1.0) = 0
  3. 计算置信度 Conf1： $Conf_1 = 1 - \frac{H_1}{\ln|V|} = 1 - 0/1.386 = \mathbf{1.0}$ （即：只选一个词时，模型处于“绝对自信”状态）

第二步：计算 k = 2 时的状态

我们尝试把 w2 加入候选集，此时 S2 = {w1, w2}。

  1. 局部归一化（让这俩词概率和为 1）： 总和 Sum = 0.80 + 0.15 = 0.95 P′(w1) = 0.80/0.95 ≈ 0.842 P′(w2) = 0.15/0.95 ≈ 0.158
  2. 计算局部熵 H2： H2 = −(0.842 × ln 0.842 + 0.158 × ln 0.158) H2 ≈ −(−0.145 − 0.292) = 0.437
  3. 计算局部置信度 Conf2： Conf2 = 1 − 0.437/1.386 ≈ 0.685
  4. 计算增量置信度 ΔConf： ΔConf = (Conf2 − Conf1)/ln |V| ΔConf = (0.685 − 1.0)/1.386 ≈ −0.227

第三步：计算 k = 3 时的状态（加入噪声词）

此时 S3 = {w1, w2, w3}。

  1. 局部归一化： 总和 Sum = 0.80 + 0.15 + 0.04 = 0.99 P′(w1) ≈ 0.808,  P′(w2) ≈ 0.152,  P′(w3) ≈ 0.040
  2. 计算局部熵 H3： H3 = −(0.808ln 0.808 + 0.152ln 0.152 + 0.040ln 0.040) ≈ 0.584
  3. 计算局部置信度 Conf3： Conf3 = 1 − 0.584/1.386 ≈ 0.579
  4. 计算增量置信度 ΔConf： ΔConf = (Conf3 − Conf2)/ln |V| ΔConf = (0.579 − 0.685)/1.386 ≈ −0.076
候选集大小 k 包含词 局部熵 Hk 局部置信度 Confk ΔConf (边际代价)
1 {w1} 0 1.0 N/A
2 {w1, w2} 0.437 0.685 -0.227
3 {w1, w2, w3} 0.584 0.579 -0.076
  • 斜率变化 ：当从 k = 1 到 k = 2 时，由于 w2 有 15% 的概率，它是一个很强的竞争者，加入它会导致置信度“剧烈跳水”（−0.227）。
  • 信息饱和 ：当加入 w3 时，由于它概率只有 4%，虽然它也会让置信度下降，但下降的幅度（−0.076）远没有加入 w2 时那么夸张。
  • 决策边界 ：算法会设定一个阈值 η。
    • 如果你希望模型 严谨 （如 Text-to-SQL），你会设定一个较小的 η，一旦 ΔConf 的跌幅超过阈值，就停止添加。
    • 如果你希望模型 发散 ，你会允许更深的跌幅。

与固定大小的Top-k或固定概率和的Top-p相比，自适应解码根据实际情况动态调整候选集大小：

  • 对于高熵（低确定性）分布，候选集会较大，增加文本多样性
  • 对于低熵（高确定性）分布，候选集会较小，保持文本连贯性

这种动态适应能力使得生成的文本既有多样性又保持连贯性，更接近人类写作风格。

实验中，η=0.0005到0.001之间能平衡多样性和连贯性

DQO（Diversity Quality Optimization，多样性质量优化）

openreview.net/pdf?id=v74LJpeUYX

核心思路是利用数学中的 行列式点过程（DPP），将“多样性”转化为几何上的“体积”来衡量 。

在大模型后训练阶段，常用的强化学习（如 PPO 或 GRPO）会引导模型去追逐最高奖励的那个“标准答案” 。结果就是模型虽然变聪明了，但说话越来越像机器人，失去了创造力和多样性 。

如何量化“多样性”？

这是 DQO 的数学基础。它将一组回答的相似度矩阵化，然后计算其行列式。

Div(y1 : k) = det (Lϕ(y1 : k))  

  • y1 : k ：模型对同一个问题生成的 k 个不同的回答 。
  • Lϕ ：相似度矩阵（Gram 矩阵）。矩阵中的每个元素 Lij 表示第 i 个回答和第 j 个回答之间的语义相似度。
  • det (⋅) ：行列式。在几何上，这个行列式代表了这些回答的向量在语义空间中所围成的平行多面体的体积。

💡 具体数据示例：

假设模型收到的提示词是：“推荐一个旅游城市”。模型生成了 3 个回答：

  1. y1: “东京（繁华，美食多）”
  2. y2: “大阪（热情，文化浓）”
  3. y3: “巴黎（浪漫，艺术之都）”

场景 A（缺乏多样性）： 如果 y1 和 y2 的语义向量非常接近（都在描述日本城市），那么它们在空间中几乎重合。这时，它们围成的“体积”（行列式值）就会非常小，甚至接近 0 。

场景 B（高多样性）： 如果回答涵盖了亚洲、欧洲等完全不同的文化特征，向量在空间中指向不同方向，围成的“体积”就会很大。DQO 的目标就是让这个体积最大化

训练目标函数

这是模型学习时的“指挥棒”。它要求模型同时优化质量、多样性和稳定性 。

$$ J_{Div}(\pi_{\theta}) = \mathbb{E}_{x, y_{1:k}} \left[ \sum_{i=1}^{k} r(x, y_i) + \alpha \log \det(L_\phi(y_{1:k})) - \beta KL(\pi_\theta || \pi_{ref}) \right] \quad \text{} $$

  • ∑r(x, yi) ： 质量项 。希望这 k 个回答的奖励值（得分）尽可能高 。
  • αlog det (⋅) ： 多样性项 。α 是调节参数。这部分强制要求这组回答之间不能太像 。
  • βKL(⋅) ： 稳定性项 。防止模型跑偏，不要离原始模型太远 。

Leave-one-out (loo) 梯度估计

在实际训练中，直接计算行列式的梯度很不稳定（如果回答完全一样，行列式为 0，log (0) 会爆炸）。作者引入了一个极其精妙的稳定化技巧：

y1, ..., yk by y1 : k $ {y_1, . . . , y_{i-1}, y_{i+1}, . . . , y_k}$ by y−i.

$$ \nabla^{loo} J_{Div}(\pi_{\theta}) = \mathbb{E} \left[ \sum_{i=1}^{k} \nabla \log \pi_{\theta}(y_i|x) \left( r(x, y_i) + \alpha \log \frac{\det(L(y_{1:k}) + I_k)}{\det(L(y_{-i}) + I_{k-1})} \right) \right] \quad \text{} $$

  • L + I ：给矩阵加上单位阵。这相当于给多样性设了一个“底线”，避免数值崩溃 。
  • $\frac{\det(L_{全部})}{\det(L_{除去当前项})}$ ：这被称为“留一法”。它衡量的是：“如果把第 i** 个回答加入这组回答，它能贡献多少额外的新信息（体积增量）？”**。

💡 数据逻辑：

如果模型已经生成了“东京”和“京都”，现在要生成第三个。

  • 如果第三个又是“大阪”，它带来的新“体积”很小，这一项的分值就低。
  • 如果第三个是“巴黎”，它带来了巨大的新“体积”，分值就高，模型就会倾向于生成这种回答。

DDPrompt 差异化多样性提示策略

https://aclanthology.org/2024.acl-short.17

核心思想

传统的 Zero-Shot-CoT 往往使用统一的提示词（如 “Let’s think step by step”）来处理所有问题，但这种“一刀切”的方法忽略了不同类型题目（如算术、逻辑、常识）对引导语的敏感度差异 。DDPrompt 的核心在于：针对不同特性的问题，自动匹配最适合的提示语集合，并通过多路径推理提高准确率。

技术架构

论文将该方法分为两个主要阶段：

  • 阶段一：GOTSS (生成最优触发句集)
    • 问题聚类 ：利用 Sentence-BERT 将题目转化为语义向量，再通过 K-Means 算法将题目分为 m 个簇（Clusters） 。
    • 策略筛选 ：从预设的 14 个触发句中，针对每个簇测试并挑选出准确率最高的 k 个触发句（Top-k），形成该类题目的“最优集合” 。
  • 阶段二：推理 (Inference)
    • 动态匹配 ：对于新输入的问题，计算其与各聚类中心的 余弦相似度 ，将其归入最相似的类别 。
    • 并行推理 ：调用该类别对应的 k 个最优触发句，让大模型生成 k 个不同的推理路径 。
    • 多数投票 ：通过 Majority Voting 从多个结果中选出最终答案，增强预测的鲁棒性 。